
1. 확률
1. 부울의 부등식 (Boole's inequality)
- 사건들의 합집합의 확률이 각 사건들의 확률의 합보다 작거나 같음


여러 개의 사건들
P(Aᵢ) : 각 사건 Aᵢ의 확률

: 각 사건의 확률을 합한 값
2. 본페로니 부등식 (Bonferroni's inequality)
- 사건들의 합집합 확률을 구할 때,
상한선과 하한선을 제공함

2. 조건부확률
1. 조건부확률 (Conditional probability)
- 확률실험에서 새로운 정보나 조건이 추가되었을 때, 사건 B의 확률

P(B|A) : 사건 A가 발생한 조건 하에서 사건 B가 발생할 확률
P(A∩B) : 사건 A와 사건 B가 동시에 발생할 확률
P(A) : 사건 A가 발생할 확률 (단, P(A) >0)
2. 사망률 (Mortality rate)
- 특정 기간 동안 일정 인구 집단에서 발생한 사망의 비율
ex) 60세 이상의 사망률
→ 표본공간이 전체연령대에서 60세 이상으로 축소
3. 생존률 (Survival rate)
- 특정 기간 동안 특정 집단에서 살아남은 사람의 비율
4. 완전생명표
- 인구 집단에 생애동안 발생할 수 있는 사망률, 생존률 등
통계적 데이터를 체계적으로 나타낸 표
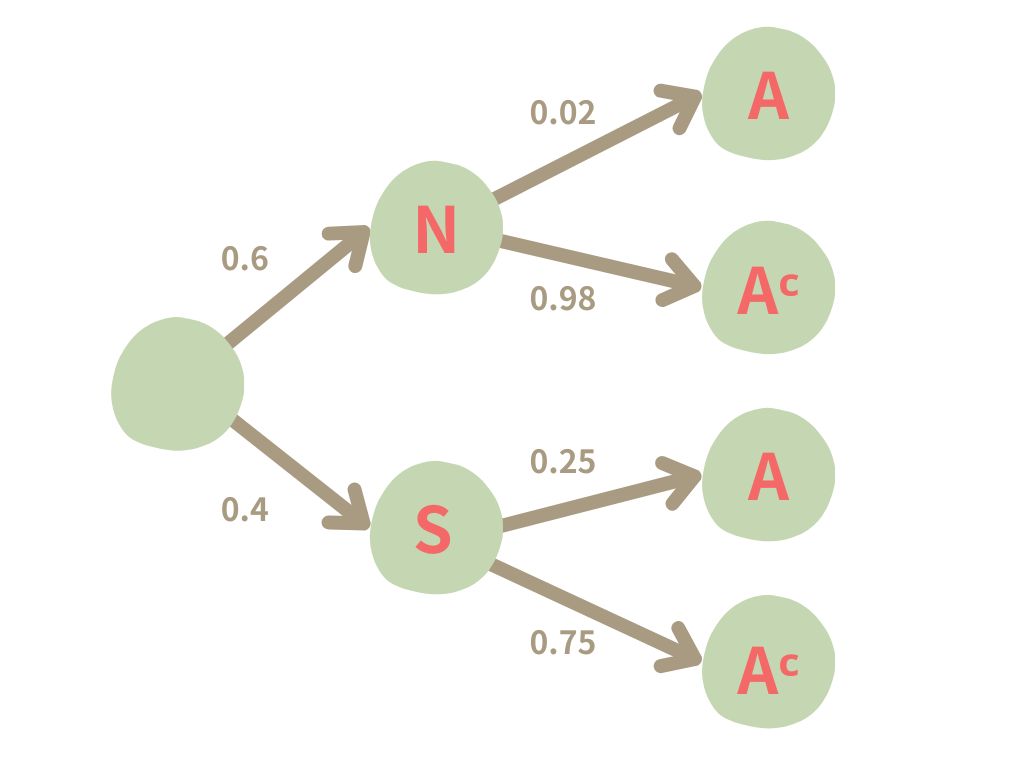
5. 확률수형도 (Probability tree)
- 사건들의 조건부확률과 결합확률을 시각적으로 나타냄
- 각 사건이 일어날 확률을 가지는 분기점을 통해 사건의 발생경로를 나타내며,
가능한 모든 결과를 구체적으로 보여줌
6. 표본공간의 분할 (Partition)
- 표본공간을 여러 개의 부분 집합으로 나누는 것
① 상호 배타적 (Mutually Exclusive)
- 각 부분집합은 다른 부분 집합과 겹치지 않음
A∩B=∅
② 전체를 이루는 사건 (Exhaustive)
- 각 부분집합들의 합집합은 전체 표본공간과 같아야 함
A₁ ∪ · · · ∪Aₙ = Ω
3. 독립사건 (Independent events)
1. 독립사건 (Independent events)
- 두 사건이 서로 영향을 미치지 않는 경우
- 두 사건 A와 B가 동시에 일어날 확률은 각 사건의 확률을 곱한 것과 같음
P(A∩B) = P(A) P(B|A) = P(B) P(A|B)
ex) 동전 던지기와 주사위 굴리기
① 각 사건의 확률
- 동전 던지기에서 앞면이 나올 확률 : 1/2
- 주사위에서 3이 나올 확률 : 1/6
② 두 사건이 동시에 일어날 확률
P(앞면∩3) = P(앞면) · P(3) = 1/2 · 1/6 = 1/12
4. 베이즈정리 (Bayes' theorem)
1. 베이즈정리 (bayes' theorem)
- 조건부확률을 이용하여 어떤 사건이 발생했을 때
다른 사건의 확률을 계산하는 방법
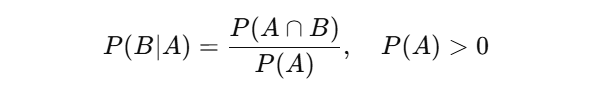
P(B∣A) : 사건 A 조건 하에서 사건 B가 발생할 확률 (先 A)
P(A∩B) : 사건 A와 사건 B가 동시에 발생할 확률
P(A) : 사건 A가 발생할 확률
ex) 질병 진단
사건 A : 어떤 사람이 질병을 가지고 있음
사건 B : 그 사람이 특정 증상을 보임
2. 코호트 연구 (Cohort study)
- 특정 인구 집단(코호트)을 일정기간 동안 추적하여
특정 요인이 질병이나 사건 발생에 미치는 영향을 분석하는 관찰연구의 한 유형
- 인과관계를 밝히는 데 효과적
3. 전향적 코호트 연구 (Prospective study)
- 현재로부터 미래로 추적 [원인 ⇒ 결과]
ex) 흡연과 폐암의 연관성 연구
ex) 식단과 심혈관 질환 연구
4. 사전확률 (Prior probability)
- 원인의 가능성인 P(A) 또는 P(Aᶜ)는 사건 B가 관측되기 이전의 확률
- 새로운 데이터를 반영하면 사후확률로 업데이트됨
ex) 동전을 던질 때 앞면이 나올 확률은 1/2
5. 사례-대조연구 (Case-Control study)
- 특정 질병이나 사건의 발생여부를 기준으로
두 집단을 비교하여 원인 또는 위험요인을 분석하는 역학 연구방법
- 후향적 연구 (Retrospective study) : 과거 데이터로 원인을 추정
ex) 흡연과 폐암의 관계
① 사례군 : 폐암 환자
② 대조군 : 폐암이 없는 환자
③ 두 집단의 과거 흡연 이력을 조사하여 흡연이 폐암 발생에 미치는 영향 분석
6. 사후확률 (Posterior probability)
- 특정 사건이 발생한 후 새로운 정보를 바탕으로 해당 사건의 확률을 갱신한 값
'데이터 사이언스' 카테고리의 다른 글
| 기초통계학 8 | 분산, 표준편차, 결합분포와 주변분포, 베르누이 시행과 확률변수 (0) | 2025.01.07 |
|---|---|
| 기초통계학 7 | 확률변수, 확률질량함수, 확률밀도함수, 기댓값 (0) | 2025.01.06 |
| 기초통계학 5 | 확률, 경우의 수, 통계적 확률 (0) | 2025.01.05 |
| 기초통계학 4 | 분할표, 비교그림, 산점도, 공분산 & 상관계수 (0) | 2025.01.04 |
| 기초통계학 3 | 자료의 중심위치, 산포, 분포 형태 분석 (0) | 2025.01.04 |



