
1. 수치를 이용한 자료정리
- 중심위치
- n개의 수치자료 x₁, x₂, x₃, ... , xₙ
- xᵢ : i 번째 표본의 값 (관측값)
- n : 표본 크기 (Sample size)
1. 표본평균 (Sample mean)
- 주어진 표본 데이터의 평균
- 전체 모집단을 조사할 수 없는 경우,
모집단 특성을 유추할 때 사용

2. 표본비율 (Sample proportion)
- 표본 데이터에서 특정 조건을 만족하는 비율
- y = x₁ + x₂ + x₃ + ... + xₙ (해당 범주에 포함된 표본의 수)
- 표본비율 = y/n

3. 이상점 (Outlier)
- 데이터셋에서 다른 값들과 크게 벗어난 데이터 값
- 다양한 원인으로 평균이나 표준편차 계산에 영향을 주어
왜곡될 수 있기 때문에 주의해야함
- 이상점을 대체할 수 있는 통계값 : 중앙값, 절사 평균, 최빈값 등
4. 기하평균 (Geometric mean)
- 데이터의 곱셈적 관계를 반영한 평균
- 특히 비율이나 성장률 다룰 때 유용함


ex) 1인당 총소득의 연평균 증가율 구하기
① 상황
- 1990년 200만 원
- 2020년 305만 원
② 기하평균 계산

1. 값 대입


2. 증가율 계산

⸫ 평균 연평균 증가율은 약 1.42%
5. 조화평균 (Harmonic mean)
- 관측값의 역수의 평균을 구하고 다시 역수로 변환한 값

ex)
두 구간을 이동하는 자동차의 평균 속도 계산
① 상황
- 첫 번째 구간: 60 km/h로 이동
- 두 번째 구간: 40 km/h로 이동
② 평균속도 계산


⸫ 평균속도는 48km/h
6. 표본중앙값 ( = 표본중위수) (Sample median)
- 데이터를 크기 순서대로 정렬했을 때 가운데 있는 값
- 극단값에 영향받지 않고 데이터의 중간 위치를 나타내기 때문에
평균과는 다름
- 이상점의 유무에 관계없이 안정적인 중심위치 제공 → 이상점에 로버스트(Robust)하다
ex)
데이터 : 30, 35, 40, 95, 100
- 중앙값 (Median) = 40
- 평균 (Mean) = (30 + 35 + 40 + 95 +100) / 5 = 60
7. 순서통계량 (Order statistics)
- 데이터를 크기 순서대로 정렬한 후 각 값의 순위를 매긴 값
- 표본을 오름차순으로 정리한 것
8. 표본절사평균 (Sample trimmed mean)
- 데이터에서 극단값을 제외하고 나머지 값들의 평균 계산
- 데이터를 정렬하고, 양쪽 끝에서 일정비율을 잘라내고
나머지 데이터의 평균을 구함
- 데이터 분포가 비대칭일 때의 이상치 영향을 제거함
ex)
데이터 : 1, 2, 3, 4, 5, 6, 7, 8, 9, 100
① 데이터 정렬 : 1, 2, 3, 4, 5, 6, 7, 8, 9, 100
② 10% 절사 : 2, 3, 4, 5, 6, 7, 8, 9
③ 평균 계산 : (2 + 3 + 4 + 5 + 6 + 7 + 8 + 9) / 8 = 5.5
⸫ 10% 절사평균은 5.5
9. 표본최빈값 (Sample mode)
- 자료 중 빈도가 가장 많은 값
- 다중 최빈값 (Multi-modal) : 여러개의 최빈값
- 연속자료는 없을 수도 있음
2. 산포 ( (= 퍼짐) Dispersion)
1. 산포 (Dispersion)
- 데이터가 얼마나 퍼져있는지 즉, 분산 정도를 나타내는 지표
- 분포 특성과 데이터의 변동성 측정
- 높은 산포 : 데이터 값이 평균값으로부터 멀리 떨어져 있음 → 중심위치 변동성이 큼
- 낮은 산포 : 데이터가 평균값 근처에 밀집되어 있음 → 중심위치 변동성이 작음


2. 범위 (Range)
- 데이터 집합에서 최소값과 최대값의 차이
- 데이터가 얼마나 넓게 퍼져 있는지 측정
- 범위 = 최대값 - 최소값
3. 사분위(간)범위 (Interquartile-Range, IQR)
- 동일비율로 자료를 4등분 할 때의 세 위치
- 극단값(이상치)에 영향을 덜 받기 때문에
중앙 분포만 보고 싶을 때 용이함
- 제1사분위수(Q1) : 25% 지점
- 제2사분위수(Q2) : 50% 지점 = 표본중앙값
- 제3사분위수(Q3) : 75% 지점
4. 표본분산 (Sample variance)
- 데이터가 평균으로부터 얼마나 퍼져 있는지 나타내는 지표
- 분산이 큼 : 데이터가 평균을 기준으로 넓게 퍼져있음
- 분산이 작음 : 데이터가 평균 주변에 모여있음
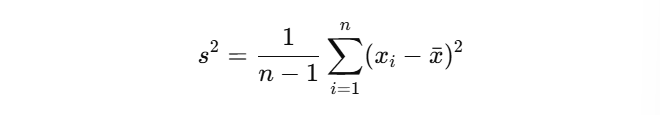
- n-1 : 자유도 (Degree of freedom)
- 통계적 추론 : 표본에서 모집단의 분산을 추정할 때, n-1을 사용하면, 비편향추정량이 됨
- 비편향추정량 : 표본분산의 기대값이 모집단의 실제분산과 같도록 보정된 추정량
5. 표본표준편차 (Sample standard deviation)
- 데이터가 평균 기준으로 얼마나 퍼져있는지 나타내는 지표
- 표본분산의 제곱근
- 원래 데이터와 동일해서 직관적으로 데이터 분포 이해하는데 유용함

6. 표준화 (Standardization)
- 데이터를 비교하기 쉽게 만들기 위해
서로 다른 평균과 분산을 가진 데이터를 동일한 척도로 변환하는 과정
- 변환된 데이터는 평균이 0
- 표준편차가 1인 표준정규분포(Standard Normal Distribution)를 따름
- 측정단위에 영향받지 않도록 중심위치와 척도를 조정해 절대비교 가능

7. 변동계수 (Coefficient of variation)
- 데이터의 표준편차를 평균으로 나눈 값
- 표준편차만 이용해서 산포를 비교하면 적절하지 않기 때문에
평균으로 표준편차를 보정함
- 데이터의 상대적인 변동성을 나타냄
- 데이터의 평균 크기에 비해 얼마나 변동이 큰지 확인할 때 유효함
- 변동계수 값이 큼 : 데이터 변동성이 크고, 평균에 비해 데이터가 많이 퍼져있음
- 변동계수 값이 작음 : 데이터 변동성이 작고, 평균에 비해 데이터가 덜 펴져있음

3. 분포의 형태
- 분포는 모양과 중심, 퍼짐 정도, 대칭 여부 등을 기반으로 분류됨
1. 대칭분포 (Symmetric Distribution)
- 많은 통계분석 방법은 중심위치를 기준으로 모집단이 대칭이라고 가정
- 평균, 중앙값, 최빈값이 같음

2. 왜도 (Skewness)
- 분포가 한쪽으로 치우친 형태
- 피어슨(Karl Pearson) 제안
- 왜도의 값에 따른 분포 형태
① 0에 가까움 : 대칭분포 (정규분포)
② 양수 : 꼬리가 오른쪽(양수방향)으로 길다 → 우측 왜도
③ 음수 : 꼬리가 왼쪽(음수방향)으로 길다 → 좌측 왜도



3. 두터운 꼬리 (Heavy tail)
- 꼬리가 길게 분포

4.첨도 (Kurtosis)
- 꼬리 두께와 꼬리 분포 모양을 나타냄
- 분포의 중심보다는 꼬리부분이 얼마나 두꺼운지에 따라 영향을 많이 받음
- 첨도가 클 수록 뾰족한 분포인데, 극단값이 더 자주 나타날 가능성이 높음
- 첨도 값에 따른 분포모양
① 3 = 중간첨도 (Mesokurtic) : 정규분포 (꼬리가 평균적으로 두껍지도 얇지도 않음)
② 3보다 큰 값 (Positive Kurtosis) : 뾰족한 분포 (Leptokurtic)
- 데이터가 중심에 몰려있고, 꼬리가 두꺼움
- ex) 극단적인 금융데이터, 위험한 자산 분포
③ 3보다 작은 값 (Negative Kurtosis) : 평평한 분포 (Platykurtic)
- 분포가 전체적으로 넓게 퍼져있고 꼬리가 얇음

5. 왜도와 첨도 활용
- 심한 왜도, 큰 첨도를 가지면 자료에 이상점이 있을 가능성 높음
- 정규성 검정 : 데이터가 정규분포를 따르는지 확인 가능
ex)
① 금융 데이터 : 주가, 수익률 분포는 첨도가 큰 경우가 많아서(뾰족) 극단적인 손실이나 이익이 발생할 가능성을 모델링
② 의학 연구 : 데이터 분포를 확인하고 비정상적인 데이터(이상점)를 제거하거나 적합한 분석방법 선택
6. Jacque-Bera 검정
- 데이터가 정규분포를 따르는지 여부를 검정하기 위해 사용되는 통계적 방법
- 왜도와 첨도 값을 기반으로 정규성 확인


- JB검정 활용
→ 정규분포는 왜도 = 0, 첨도 = 3 (초과점도는 0)
⇒ 데이터의 왜도와 첨도가 기준에 벗어나면 정규성이 없는 것으로 간주
'Data Science > statistics' 카테고리의 다른 글
| 기초통계학 5 | 확률 · 경우의 수 · 통계적 확률 (0) | 2025.01.05 |
|---|---|
| 기초통계학 4 | 분할표 · 비교그림 · 산점도 · 공분산 · 상관계수 (0) | 2025.01.04 |
| 기초통계학 2 | 자료 분류와 특성 · 범주형 자료 · 수치자료 (0) | 2025.01.03 |
| 기초통계학 1 | 모집단 · 표본 · 표본추출방법 · 가중치 (3) | 2025.01.02 |
| 수리통계학 | 기초 용어 개념 정리 (2) | 2024.12.30 |




