1. 통계학
- 통계학 정의
- 데이터를 수집 · 분석 · 해석 · 표현하는 학문
- 연구 결과를 근거로 결론을 도출하거나 의사 결정을 돕는 역할
- 불확실한 상황에서 확률을 통해 바람직한 의사결정을 하기 위함 - 기술통계
- 자료 수집 · 정리 · 해석 - 추리통계
- 표본으로 모집단 추론 - 척도
- 데이터를 측정하기 위한 기준- 명목척도(Nominal) : 범주를 구분하기 위해 이름을 부여함 (예: 성별)
- 서열척도(Ordinal ): 순위에 따라 나눔 (예: 만족도 등급)
- 등간척도(Interval) : 간격이 일정한 임의영점와 순위를 가짐 (예: 온도)
- 비율척도(Ratio) : 절대영점을 가지고, 사칙연산 가능 (예: 무게, 길이)
2. 데이터 표현과 요약
- 빈도분포(Frequency Distribution)
- 어떤 사건이 일어나는 횟수를 조직화하여 표현 - 변산도(Variability)
- 데이터의 분산 정도 (분포가 흩어진 정도)
- 범위 사분위편차, 표준편차, 분산 등이 있으나, 표준편차와 분산을 가장 많이 사용
(수학적으로 취급용이, 표집변이가 작고, 모든 변수를 대표하기 때문)
- 분산(Variance): 데이터가 평균에서 얼마나 떨어져 있는지 나타냄.
- 표준편차(Standard Deviation): 분산의 제곱근, 데이터의 평균적 차이.
- 중심경향값(Central Tendency)
- 분포에서 변수들이 어떤 값을 중심으로 모이는 경향
- 평균값을 가장 많이 사용
(수학적으로 취급용이, 표집변이가 작고, 모든 변수를 대표하기 때문)
- 평균(Mean): 데이터의 합을 개수로 나눈 값으로, 분포의 균형 지점
- 중앙값(Median): 데이터의 가운데 값
- 최빈값(Mode): 가장 많이 나타난 값
3. 표본과 분포
- 표본분포(Sample Distribution)
- 모집단을 대표하도록 뽑힌 표본의 분포 - 표집분포(Sampling Distribution)
- 모집단에서 크기가 n인 표본분포를 무한으로 추출하여 평균분포를 나타냄
→ 중심극한 정리에 따라 n이 커지면, 표집분포가 정규분포를 따르게 됨 - 정규분포(Normal Distribution)
- 특정상황에서 취할 수 있는 이상적인 개념의 분포형태
- 대칭적이고 종 모양
- 평균을 중심으로 대칭인 단봉분포
- 평균치 = 중앙치 = 최빈치 - 자유도(Degree of Freedom)
- 데이터에서 독립적으로 변할 수 있는 자유로운 값의 수
- 표본분포(Sampling Distribution)를 구성하기 위해
자유롭게 반복해서 추출 할 수 있는 표본 수(repeated random sample)
- 보통 n-1 - 단순 무선표집 (Simple Random Sampling)
- 표집 시, 표본추출의 확률이 모두 같고
서로 독립적으로 추출되는 것
- 무선 할당 전, 참가자를 확보할 때 표집(Sampling)을
무선(Random)으로 함
- 외현적 타당성(외적 타당도) 보장됨 - 무선할당 (Random Assignment)
- 추출한 표본 중에서 실험집단과 통제집단을 나누는 것
- 참가자를 실험집단과 통제집단에 배치할 때,
무선(Random)으로 배치(Assignment)하는 것
- 내현적 타당성(내적 타당도) 보장됨
(편파될 가능성이 있어, 외현적 타당성 보장 X)
4. 가설검정
- 가설검정 순서:
- 연구가설(귀무가설(H0)과 대립가설(H1)) 설정하고 통계가설 설정
- 유의수준(α) 결정
- 검정통계법과 분포 진술
- 유의수준에 맞게 임계값 설정
- 검정통계값 계산
- 영가설 기각 여부 결정하고 결론 도출
- 영가설(H₀): 평균 차이가 없음
- 대립가설(H₁): 평균 차이가 특정 방향으로 있다 (증가 또는 감소)
- 가족분포
- 자유도에 따라 모양이 바뀌는 분포
- 표본 수(n)가 커질수록 정규분포와 가까워짐
- T분포
- 표본평균과 모평균의 차이를 비교할 때 사용
- 특히 표본 크기가 작고 모집단 분산을 모를 때 사용
- 정규분포와 유사하지만, 꼬리가 더 두꺼워 극단값을 더 많이 포함
- 자유도가 커질수록 정규분포와 비슷해짐 (좌우대칭)
- T분포
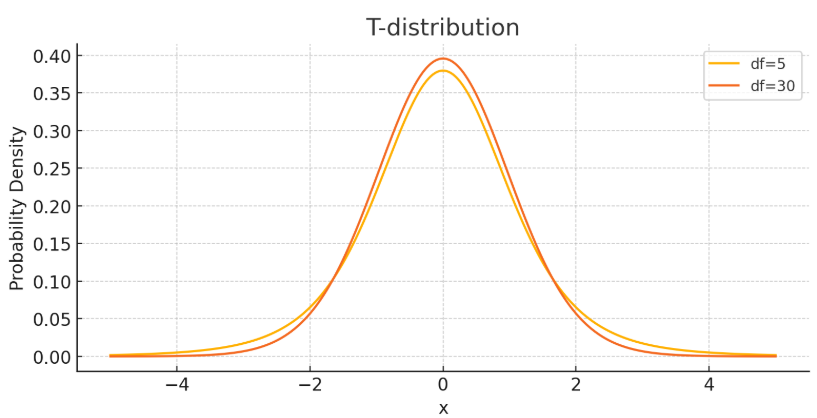
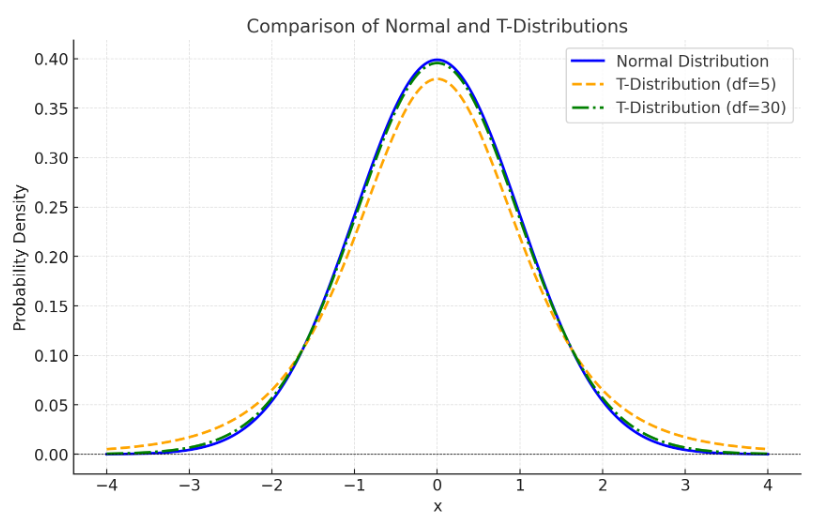
- F분포
- 두 집단의 분산 차이를 비교할 때 사용 (ex. 분산분석, ANOVA)
- 양의 값만 가짐 ( ∵ 분산은 음수가 될 수 없음)
- 오른쪽으로 긴 꼬리를 가짐
- 자유도가 커질수록 분포가 더 좁아지고 오른쪽으로 긴 꼬리를 가짐
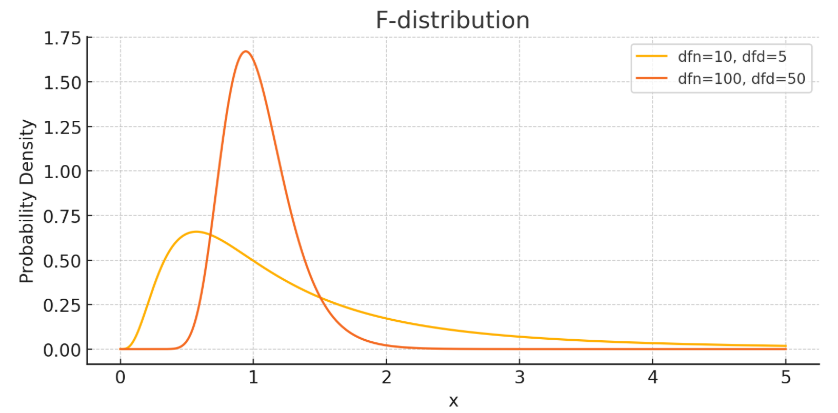
- 카이스퀘어 분포
- 독립성 검정, 적합도 검정, 분산추정에 사용
- 0 이상의 값만 가짐
- 오른쪽으로 긴꼬리를 가짐
- 자유도가 커질수록 정규분포와 비슷해짐 (좌우대칭)
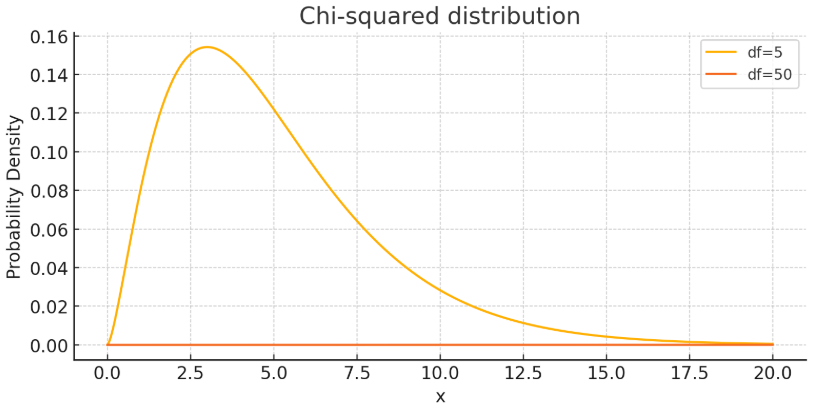
- 추정(Estimation):
- 표본으로 모집단 특성 추정
- 점추정 : 표본의 한 값으로 모집단의 특성 추정
(표본 평균이 표본분포의 어디에 위치하는지에 따라 채택역 · 기각역 확인) - 구간추정 : 신뢰구간에 따른 모집단의 예상되는 평균 범위를 구하는 것
① 점추정을 반복하지 않아도 됨
② 표본이 커지면 신뢰구간의 폭이 좁아짐 · · · > 표본에 따른 영향 확인가능 - 추리통계에서의 통계적 추론법
① 가설검증
② 추정법 (점추정, 구간추정)
- 점추정 : 표본의 한 값으로 모집단의 특성 추정
- 기각역(Rejection Region)
- 귀무가설(영가설) 기각·채택 여부 결정
- 유의수준 α인 부분 - 일종 오류(Type I Error, α오류)
- 참인 귀무가설(영가설)을 기각하고 대립가설을 설정하게 될 확률
→ 일종오류를 감수할 확률 = 유의수준 - 이종 오류(Type II Error, β오류)
- 거짓인 귀무가설(영가설)을 채택할 확률
→ 1- β = 통계적 검정력
5. 통계적 검정 및 검정의 종류
- 통계적 검정(Statistical Test)
- 가설의 진위를 검정
- 연구가설 뒷받침을 위한 통계가설을 세우고, 통계적으로 검정하는 경우
연구자 개인의 주관적 판단을 배제하고,
객관적이고 과학적인 결과 도출가능 - 통계적 검정력
- (통계적 검정에서) 대립가설이 참일 때, 영가설을 기각시킬 확률
- 표본의 수가 커지면 실제적 유의성이 없음에도 표집오차가 작아져, 영가설이 기각될 수 있음
- 표본의 수가 작으면 실제적 유의성이 있음에도 유의한 차이가 나오지 않을 수 있음 - 통계적 유의성
- 설정한 유의수준 하에서
자신의 영가설을 기각할만큼 유의한 차이가 있는가?
→ 통계적 유의성이 있다고 해서 반드시 실제적 유의성이 있는 건 아님 - 실제적 유의성
- 통계적으로 유의미한 결과가 실제로도 중요한가?
- 효과 크기로 확인가능 - 효과크기(Effect Size)
- 두 평균 간 차이를 통합된 표준편차로 나누어 얻은 지수
(평균차의 크기 평가 시, 두 표본의 표준편차를 통합해서 사용)
- 단순히 차이유무만 보는 게 아니라,
그 차이가 실제로 얼마나 중요한지를 평가함
- 통계에서는 유의미한 차이가 있어도 실제 차이가 아주 작을 수 있기 때문에,
실제적 유의성과 통계적 유의성 모두 고려해야 함
ex. 두 반의 시험점수 비교
더보기
- 반 A의 평균 점수: 80점
- 반 B의 평균 점수: 70점
- 두 반의 표준편차가 각각 5점과 10점이라고 가정
- 단순 평균 차이:
두 반의 평균 차이는 80−70=1080 - 70 = 10점
이 차이가 단순히 통계적으로 유의미한지만 확인하면,
실제로 큰 차이인지 알 수 없음 - 효과크기 계산
- 효과크기의 의미:
- 효과크기 d=1.33d = 1.33은 매우 큰 차이를 의미합니다.
- Cohen's 기준:
- d=0.2d = 0.2: 작은 효과.
- d=0.5d = 0.5: 중간 효과.
- d=0.8d = 0.8: 큰 효과.
- 통계적 검정력 (Power)
- 귀무가설이 거짓일 때 올바르게 기각할 확률
- 통계력이 높을수록 실험이나 분석의 신뢰도 높아짐
[쉬운 설명]
귀무가설이 거짓인데도 기각하지 않으면,
중요한 결과를 놓치는 2종오류가 발생함
→ 통계력은 이런 오류를 피하고,
실제로 효과나 차이가 있을 때,
이를 정확히 알아차리는 능력을 뜻함
ex. 약의 효과를 검증하는 실험
- 귀무가설 : 약은 효과가 없다
- 대립가설 : 약은 효과가 있다
→ 실제로 약이 효과가 있을 때, 귀무가설을 기각하는 확률이 통계력임
- 통계적 검증력 높이는 법
① 효과크기가 클 때 (영가설과 실제 평균 차이가 크면 차이를 더 쉽게 발견함)
② 일방가설 사용 (방향성을 미리 정하면, 검정의 집중도 높아짐)
③ 유의수준 크게 설정 (유의수준을 높이면 기각수준이 느슨해져, 귀무가설을 더 쉽게 기각가능)
④ 표본 크기 증가 (표본크기가 크면 → 표준오차가 작고 → 통계검정값이 커져서 → 영가설이 기각될 확률 높아짐)
- T검정(T-test)
- 두 집단 간 평균을 비교하기 위해 사용하는 통계방법
(단일표본 T검정, 두 독립표본 T검정(통합분산 사용), 두 종속표본 T검정(T검정보다 직접차이 계산법사용))
- 모집단의 분산과 표준편차를 모를 때 사용함
→ 모집단의 분산을 모르기 때문에 표본의 분산을 모집단 분산 추정치로 사용
(이때, 편파되는 것을 방지하기 위해 자유도 n-1에 해당하는 표본의 분산을 사용)
[쉬운 설명]
- 데이터를 분석할 때, 모든 사람(모집단)의 데이터를 전부 알 수 없기 때문에,
모든사람(모집단) 대신에 일부사람(표본)을 뽑아 데이터를 분석함
이 경우, 표본의 결과만 나오게 됨
∴ 표본의 결과만 보고 판단하는 게 아니라,
통계적으로 신뢰할 수 있는 결과인지 검증하는 게 T검정
쉽게 말해, 'A집단과 B집단의 평균이 정말 다를까?'를 알아보는 방법 - 단일표본 T검정 (One-Sample T-test)
- 하나의 집단 평균을 기준값과 비교
ex. 어느 학교 학생들의 평균시험점수(비교집단)가 80점(기준값)과 다른지 비교 - 독립표본 T검정 (Independent-Sample T-test)
- 서로 다른 두 집단의 평균 비교
ex. 남학생과 여학생의 평균키가 다른지 비교
- 독립표본 T검정의 기본가정
① 모집단이 정규분포 (표본 수가 많아지면(관측갯수 30개 이상) 일반적으로 정규분포에 가까워짐)
② 동분산 가정 충족 (두 집단의 분산이 비슷해야함)
③ 두 표본들은 독립적 (ex. 남학생, 여학생처럼 서로 영향 미치지 않음) - 대응표본 T검정 (A Paired Sample T-test)
- 같은 집단의 두 조건에서 평균 비교
- 표본의 각 사례마다 대응하는 2개의 관측치가 있음
(≠ 단일표본 T검정)
ex. 체중감량 운동프로그램 효과를 알아보기 위해
프로그램 시작 전 체중(A)과 프로그램 종료 후 체중(B)를 측정해서
운동 전 후 체중 평균차이가 통계적으로 유의미한지 비교
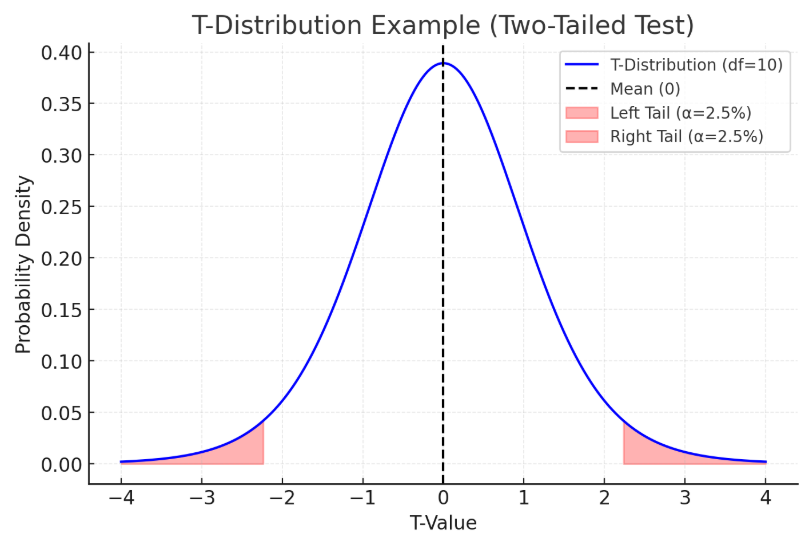
- 양방검정 (Two-tailed Test)
- 두 집단 평균의 차이가 있는지 검정
(어느 방향이든 단순히 차이가 있는지에 초점)
- 기각역(유의수준)이 분포의 양쪽 끝에 분포
- 평균 차이가 어디로 발생할지 모를 때 사용
- 일반적인 연구에 적합하며, 방향성을 가정하지 않는 경우 주로 사용
ex. 신약 개발 시, 약효가 더 좋아질 수도 있고 나빠질 수도 있는 경우 - 일방검정 (One-tailed Test)
- 효과의 방향을 사전에 가정할 때 사용
- 기각역(유의수준)이 분포의 한쪽 끝에만 집중
- 기각역이 한쪽에 집중되므로, 기각값이 작아져
영가설 기각이 더 용이함
- But, 실제차이가 가정과 반대 방향으로 나타나면,
검증력이 떨어져 오류 발생 가능성 증가
ex. 신약이 기존 약보다 혈압을 낮출 것이라고 가정한 경우 - 양방검정과 일방검정 선택 기준
- 양방검정
- 방향성을 알 수 없는 상황에서 사용
- 안전하고 보편적 - 일방검정
- 연구·실험의 명확한 방향성이 있을 때 사용
- 사전정보나 가설이 충분히 뒷받침되어야 하고 신중해야함 - 양방검정은 평균 차이가 어디서든 발생할 가능성을 고려하고,
일방검정은 특정방향으로 발생할 가능성을 가정하는 검정방식
- 양방검정
- Z검정
- 모집단의 분산과 표준편차를 알고 있을 때,
집단 간 평균 차이를 비교
- Z검정의 가정
① 양적변수여야 함 (키, 점수 · · ·)
② 모집단의 분포가 정규분포
③ 등분산 가정 (두 집단의 분산이 비슷해야 함) - T검정과 Z검정의 차이
- T검정 : 표본 크기가 작고 분산을 모를 때 사용
- Z검정 : 표본 크기가 크고 분산을 알고 있을 때 사용
- F검정 (F-test)
- 세 집단 이상의 평균 차이를 비교할 때 사용
- 모집단의 분산과 표준편차를 모를 때 사용
- ANOVA = 분산검정 = F검정
ex. 3가지 공부 방법의 효과 비교
서로다른 3가지의 공부방법을 사용한 세그룹(A, B, C)의 학생들이 있음
각 그룹의 시험점수 평균을 비교해, 효과적인 공부방법 찾기
① 집단 간 분산 : A, B, C 세그룹의 평균 점수가 얼마나 다른지 비교
→ A의 평균 : 80 | B의 평균 : 75 | C의 평균 : 70
⇒ 집단 간 평균점수 차이가 큼
② 집단 내 분산 : 각 그룹의 학생들이 평균점수 주변에서 얼마나 분포됐는지 확인
→ A의 분포 : 70-90 | B의 분포 : 60-90 | C의 분포 : 70-80
⇒ 각각 고르게, 넓게, 좁게 분포함
③ 처치효과 판단
- 만약 집단 간 분산이 집단 내 분산보다 크다면,
세가지 공부 방법이 서로 다르게 효과가 있다는 뜻
즉, 어떤 공부방법이 더 효과적이라고 결론 내릴 수 없음
④ F검정 과정
- 영가설(H₀): 세 공부 방법은 모두 효과가 같다 (즉, 평균 점수 차이가 없다)
- 대립가설(H₁): 세 공부 방법의 평균 점수는 적어도 하나는 다르다
- F값을 계산해서, 이 값이 특정 임계값보다 크다면
영가설을 기각하고 공부 방법에 차이가 있다는 결론을 내림
⑤ 사후분석
- 만약 F검정에서 차이가 있다고 나왔다면,
어떤 두 집단 간 차이가 있는지 추가적으로 확인하는 사후분석 진행
ex. A와 B 비교, A와 C 비교, B와 C 비교 - 독립변수 수에 따른 F검정 종류
- 일원분산분석 (One-way ANOVA)
- 독립변수가 1개일 때 사용
ex. 공부방법이 다른 세 그룹의 평균 비교 - 이원분산분석 (Two-way ANOVA)
- 독립변수가 2개 이상일 때 사용
- 독립변수 간 상호작용도 함께 분석 가능
ex. 공부방법 + 성별의 영향을 동시에 분석
- 일원분산분석 (One-way ANOVA)
- 카이스퀘어(Chi-Square)
- 두 범주형 변수에 대한 분석방법
- 실제 관찰된 데이터(관찰빈도)와
가정에 따른 예측 데이터(기대빈도)의 차이를 분석하는 검정방법
- 전집의 상대적 빈도, 비율에 관한 추론을 다루는 빈도자료를 위한 검증통계치
ex. 동전 100번 던지기
① 결과 예상 → 앞 : 뒤 = 50 : 50
② 실제 결과 → 앞 : 뒤 = 70 : 30
③ 예상과 실제 결과의 차이가 우연인지, 실제로 의미있는 차이인지 판단함
6. 분산분석(ANOVA)
- ANOVA
- 세 집단 이상의 평균 비교
- 독립변수가 1개, 측정집단이 3개 이상인 경우,
집단 간 차이가 유의미한지 판단 - 사후검정(Post Hoc Test)
- ANOVA에서 어떤 집단 간 차이가 유의미한지 추가 검정 - ANOVA를 T검정으로 할 때 문제점
- 여러 집단을 비교할 때, T검정을 여러번 사용하면 오류 가능성 증가
(실제로는 차이가 없는데 계속 검증할 경우, '유의한 차이'를 얻게될 가능성이 높아짐) - ANOVA에서 사후검정이 필요한 이유
- F검정의 역할
- 집단 간 차이가 있는지 확인
- 그러나 F검정만으로는 어떤 집단 간 차이가 있는지 알 수 없음
- 사후검정으로 구체적인 차이 분석 필요 (ex. Tukey's HSD검증) - But, 사후검정에선 유의수준 감소
- 전체 대비수로 유의수준을 나누기 때문에 유의수준 나눠져서
통계적 유의성 낮아짐 - 사전분석 (Pre-planned analysis)
- 연구자의 연구적 배경이 강할때는 F통계값을 구하지 않고도
관심있는 대비만을 선택해서 검정하는 것
- 관심있는 대비만으로 유의수준을 나누기 때문에
사후검정에 비해 검정력 높아짐
- F검정의 역할
| 항목 | 사전분석 | 사후분석 |
| 분석시점 | F 검정 전에 관심집단만 검정 | F 검정 후 차이를 확인하기 위해 검정 |
| 검정대상 | 연구자가 설정한 특정 대비 | 모든 집단 간 대비 |
| 검정력 | 높음 | 낮음(유의수준을 나누기 때문) |
| 적합한 상황 | 명확한 연구가설이 있는 경우 | 가설없이 집단 간 차이를 탐색하는 경우 |
- 에타제곱 (η²)
- 분산분석(ANOVA)에서 사용하는 개념
- 전체 변화량 중 얼마나 많은 부분이 독립변수로 설명되는가?
- 예를 들어, 실험에서 처치(조작, 실험변수)가
결과에 얼마나 영향을 미치는지 비율을 나타냄
- 높은 에타제곱 값은 독립변수가 종속변수에 큰 영향을 미친다는 뜻
- 독립표본에서 동분산 가정이 이루어지지 않는 경우
(독립표본 T검정에서 두 표본의 분산이 같다는 가정이 깨질 때 발생하는 문제)
- 동분산 가정이 맞는 경우,
두 표본의 통합분산을 사용해 T통계값 구함
- 동분산 가정이 안 맞는 경우,
두 표본의 자유도를 조정해서 T통계값을 다시 계산함
- 독립표본에서 동분산 가정이 이루어지지 않는 경우
- 이원분산분석 (Two-way ANOVA)
- 2개의 독립변수가 있을 때 사용하는 분산분석
- 교차설계 (Crossed Design)
- 두 독립변수 각각의 주효과와 상호작용 효과 분석
ex. 공부법과 수면시간이 시험점수에 미치는 영향
① 독립변수(IV) : 공부법 , 수면시간(6시간, 8시간)
② 종속변수(DV) : 시험점수
→ 주효과 : 공부법과 수면시간이 각각 시험점수에 어떤 영향을 주는지 확인
⇒ 상호작용효과 : 공부법과 수면시간이 함께 시험점수에 영향을 미치는지 확인 (ex. 8시간 자고 인강을 보면 효과가 좋다처럼 두 요인의 조합이 다른 영향을 줄 수 있음) - 내제설계 (Nested design)
- 한 독립변수 각 수준에서 다른 변수의 영향 분석
- 상호작용 효과는 고려하지 않음
ex. 공부법이 시험점수에 미치는 영향
① 독립변수 : 공부법
② 종속변수 : 시험점수
→ 주효과 : 공부법이 시험점수에 미치는 영향 분석 (다른 요인은 고려하지 않음)
- 교차설계 (Crossed Design)
7. 회귀분석
- 회귀분석(Regression Analysis)
- 회귀방정식을 이용해 한 변수로 다른 변수를 예측하는 방법
(X로 Y를 예측)
- 회귀분석은 종속변수와 관련된 독립변수를 찾거나,
독립변수들 간 관계를 이해하려는 목적
- 인과관계는 추론할 수 없음
단지 상관관계를 예측하는 방법임
- 매개변수 모델(Parametric Model)을 이용해, 변수들 간 관계를 통계적으로 추정함
다른 독립변수들은 고정시키고, 1개의 독립변수만 변화시켰을 때의
종속변수가 어떻게 변하는지 확인
ex. 공부시간(X)이 많으면 성적(Y)이 더 좋을까?
① 공부시간을 5시간으로 하면 성적을 80점으로 '예측'할 수 있음
② 단, 공부시간이 많다고 해서 반드시 성적이 잘 나온다는 보장은 없음
③ 회귀분석은 단순 예측일 뿐, 원인과 결과를 말하는 건 아님
- 단순회귀(Simple Regression)
- 하나의 독립변수와 종속변수 관계 (두 변수 간 인과관계 조사) - 다중회귀(Multiple Regression)
- 여러 독립변수와 종속변수 관계 (단순회귀분석 확장) - 위계적 다중회귀(Hierarchical Multiple Regression)
- 연구자가 독립변수를 차례대로(단계적) 투입하면서
독립변수의 상대적 영향력의 크기를 순서대로 파악하는 것
- 각 단계별 새로운 변수들과 합쳐지면서
설명력이 어떻게 변화하는지를 보는 것 - 최소자승법(Least Squares Method)
- 회귀분석에서 예측된 변수의 기대값과 실제 변수의 차이
즉, 편차의 제곱합이 최소가 되도록 하는 회귀방정식을 구하는 것
- 편차를 최소로 하여 회귀분석에서 예측력을 높이는 것
- 단순회귀(Simple Regression)
- 회귀계수(Regression Coefficient)
- 회귀분석에서 회귀방정식의 기울기
(X가 변화할 때, Y가 변하는 정도) - 회귀식 추정에 쓰이는 2가지 방법
① 최소자승화 추정 (Least Squares Estimation; LSE) : 평균과의 차이가 최소가 되도록 회귀식 추정
② Ordinaly Least Squares (OLS) : 오차(실제값과 예측값)의 제곱의 합을 최소화해 회귀식 구함
8. 상관분석
- 상관분석
- 두 변수가 함께 변화하는 정도와 선형관계 분석 - 공분산 (Covariance, Cov)
- 두 변수가 얼마나 함께 변하는지를 나타냄
- 방향은 알 수 있지만, 단위에 따라 값이 변하므로,
크기의 의미를 명확히 알 수 없음
- 이를 해결하기 위해 표준화된 상관계수를 사용 - 상관계수(r)
- 공분산을 표준화한 값으로,
단위와 무관하게 두 변수 간 관계를 나타냄
- 두 변수 간 상관관계의 강도와 방향
- 상관정도 : 절대값 크기
- 상관방향 : 부호 (+, -)
- r 의 값의 범위 = -1 ~ +1
- 기본가정과 주의점
① 선형성 : 두 변수가 선형적 관계를 가져야 함
② 동분산성 : 데이터 분산이 일정해야 함
③ 정규분포 : 두 변수의 데이터가 정규분포를 이뤄야함
④ 변수 조건 : 연속형 양적 변수여야 함
⑤ 외적값 주의 : 이상치는 상관계수 값에 큰 영향 미칠 수 있음 - 결정계수(R²)
- 두 변수가 공유하는 공통분산의 비율 (전체 변화량 중 회귀모형이 설명하는 변화량의 비율)
- 상관계수(r)의 제곱값으로 계산
- 상관이 높을수록 예측이 정확할 가능성이 커짐
- R² 의 값의 범위 : 0 ~ 1 (1에 가까울수록 예측력이 높아짐) - 상관관계와 인과관계 차이
- 상관관계가 있다고 반드시 인과관계가 성립하는 건 아님
9. 추가 개념
- 두 독립표본 T검정
- 상호독립적인 두 모집단에서 각각 표본을 추출해 평균 차이를 비교
- 조건
① 정규분포 : 두 모집단이 정규분포를 따라야 함
② 동분산성 : 동분산성을 만족한다면 통합분산을 사용해 T통계량 계산
- 종속표본 T검정
- 동일한 피험자에게 두 번 검사하거나, 짝진 표본에서 평균 차이를 비교
- 표본 간 독립성이 없어서 표준오차 계산이 독립표본보다 복잡함
- 직접차이를 계산해 짝진 점수를 하나의 분포로 취급
- 방법
① 두 표본 차이값을 계산해, 단일 표본 T검정 수행
② 차이값의 평균과 표준오차로 T통계량 계산
| 항목 | 독립표본 T검정 | 종속표본 T검정 |
| 적용상황 | 독립된 두 모집단 비교 | 동일집단 또는 짝진표본 비교 |
| 데이터 독립성 | 표본 간 독립 | 표본 간 종속관계 (짝지음) |
| 통계계산 | 통합분산 사용 (동분산성 가정) | 차이값을 단일분포로 변환 |
| 예시 | 남녀 간 시험점수 비교 | 전후 검사에서 동일 그룹의 점수 비교 |
- 외현적 타당성(External Validity)
- 표집 시, 모집단을 대표하도록 표본이 잘 추출되었는가?
- 연구 결과를 일반화할 수 있는 정도 - 내재적 타당성(Internal Validity)
연구 내에서 인과 관계가 성립하는 정도.
반응형
'데이터 사이언스' 카테고리의 다른 글
| 기초통계학 | 4. 분할표, 비교그림, 산점도, 공분산 & 상관계수 (0) | 2025.01.04 |
|---|---|
| 기초통계학 3 | 자료의 중심위치, 산포, 분포 형태 분석 (0) | 2025.01.04 |
| 기초통계학 2 | 자료 분류와 특성, 범주형 자료, 수치자료 (0) | 2025.01.03 |
| 기초통계학 1 | 모집단, 표본, 표본추출방법, 가중치 (3) | 2025.01.02 |
| 데이터 분석과 코딩 | 무료 플랫폼 (2) | 2024.12.28 |
