
1. 자료 특성
- 통계분석 방법
- 데이터를 분석할 때, 어떤 데이터를 가지고 있는지(속성)과
무엇을 알고 싶은지(목적)에 따라 적합한 방법을 선택해야함 - 자료 속성
- 질적자료 (Qualitative)
- 숫자가 아닌 범주형 데이터
- 분석방법 : 빈도분석, 교차분석 등
ex) 성별, 색상 - 양적자료 (Quantitative)
- 숫자로 측정되는 데이터
- 분석방법 : 평균, 분산, 상관분석 등
ex) 키, 몸무게
- 질적자료 (Qualitative)
- 변수 (Variable)
- 변할 수 있는 값
- 데이터의 속성
- 독립변수 (Independent Variable)
- 다른 변수에 영향을 주는 변수
- 원인 또는 조건 - 종속변수 (Dependent Variable)
- 독립변수에 영향을 받는 변수
- 결과 또는 반응
ex) 공부시간(독립변수)이 시험점수(종속변수)에 영향을 줌 - 질적변수 (Qualitative Variable)
- 범주를 나타냄
ex) 성별, 혈액형 - 양적변수 (Quantitative Variable)
- 값이 숫자이며, 계산 가능
ex) 키, 시험점수 - 일변량자료 (Univariate data)
- 1개의 변수만 있는 자료
- 분석 목적 : 분포, 중앙값, 표준편차, 최댓값, 최솟값, 범위
- 시각화 : 히스토그램, 막대그래프, 상자그림(Box Plot) · · ·
ex) 학생들의 키 데이터 : 150㎝ | 160㎝ | 170㎝ | 165㎝
분석 목적 : 평균 키 계산 또는 가장 키가 큰 학생 찾기 - 다변량자료 (Multivariate data)
- 2개 이상의 변수로 구성된 자료
- 분석 목적 : 각 변수 간 관계나 패턴
- 시각화 : 산점도, 다차원 그래프 · · ·
ex) A학생 : 160㎝, 50㎏
분석 목적 : 키와 체중의 상관관계 분석 - 관측개체 ( = 관측값(치) (Observation)
- 데이터를 수집하는 기본 단위
- 각 개체는 1개 이상의 변수값 가짐
ex) 학생 설문조사에서 관측개체 : 학생 1명
- 독립변수 (Independent Variable)
2. 자료의 분류
| 자료 (Data) |
→ | 범주형 자료 (Categorial data) |
⇒ | 명목자료 (Nominal data) |
| ⇒ | 순서자료 (Ordinal data) |
|||
| → |
수치자료 (Numerical data) |
⇒ | 이산자료 (Discrete data) |
|
| ⇒ | 연속자료 (continuous data) |
- 범주형 자료 (Categorial data)
- 몇가지 그룹으로 나누는 데이터
- 숫자가 아닌 특정 이름이나 상태를 나타냄
- 데이터의 분포를 분석하거나 그룹 간 차이를 비교
- 명목형 자료 (Nominal data)
- 순서가 없는 범주
ex) 성별, 혈액형, 출생지 - 서열형 자료 ( = 순서자료) (Ordinal data)
- 순서는 있지만, 간격이 일정하지 않음
- 범주의 순서로 상대비교 가능
- 범주화로 수치자료를 순서자료로 바꿈
ex) 설문조사 만족도(만족/보통/불만족), 학점(A/B/C/D), 비만도(저체중/정상/과체중)
- 명목형 자료 (Nominal data)
- 수치자료 (Numerical data)
- 데이터를 숫자 형태로 나타낸 자료
- 수량적 의미를 갖고, 계산과 통계적 분석에 사용가능
- 이산자료 (Discrete data)
- 값이 정수로 표현되어, 셀 수 있는 자료 (Countable data)
ex) 교통사고 건수, 자녀의 수, 발생빈도 - 연속자료 (Continuous data)
- 값이 연속적으로 나타남
- 대부분 이산화를 통해 절사된 형태임
- 척도에 따라 명목, 순서, 구간, 비율척도로 나눔
ex) 키, 시간
- 이산자료 (Discrete data)
3. 수치자료 정리
- 도수분포표 (Frequency table)
- 데이터 값이 얼마나 자주 등장하는지 요약한 표
- 데이터 분포를 쉽게 파악할 수 있도록 도와줌
- 도수 ( = 빈도) (Frequency) : 범주에 속한 관측개체의 수
- 상대도수 (Relative Frequency) : 전체 자료 중 해당 범주에 속한 자료의 비율
상대도수 = 해당범주의 관측개체 수 / 전체 관측개체 수
ex)
① 데이터 : 학생 20명의 시험 점수 : 72, 85, 88, 75, 90, 68, 80, 85, 78, 92, 88, 77, 83, 85, 90, 72, 88, 74, 81, 79
② 도수분포표
점수 구간도수 (Frequency) 상대도수 (%) 누적도수 60-69 1 5% 1 70-79 8 40% 9 80-89 8 40% 17 90-99 3 15% 20
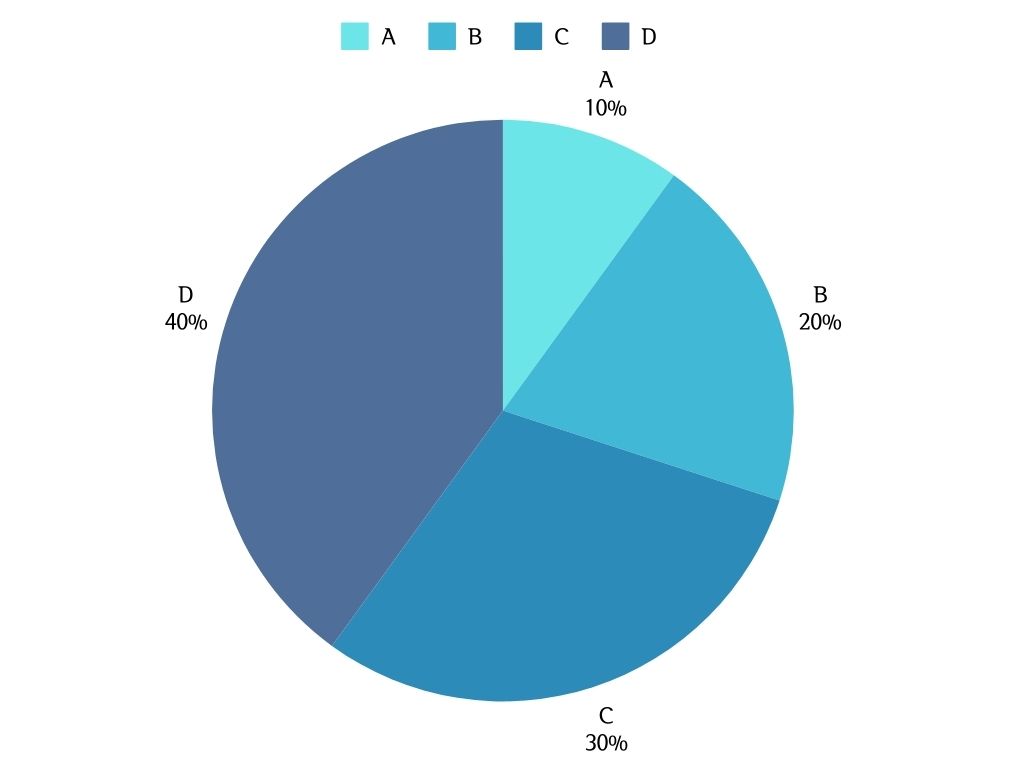
- 원도표 (Pie Chart)
- 데이터를 원형 모양으로 각 항목의 비율을 시각화함
- 각 영역의 크기는 비율에 비례함
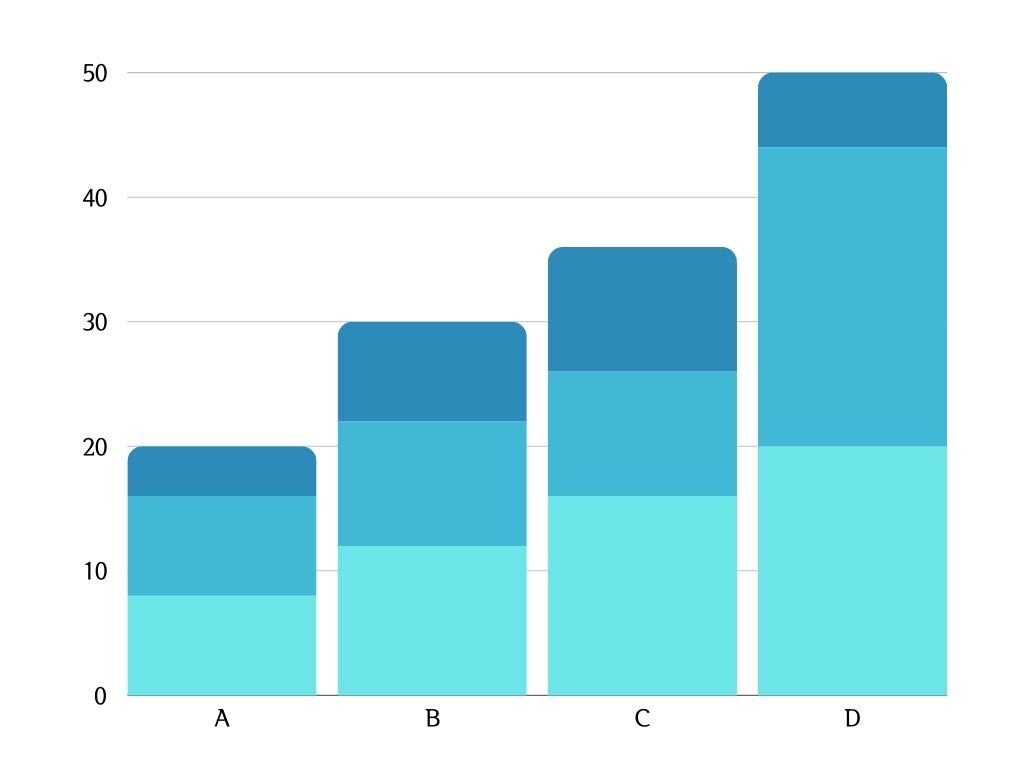
- 막대그래프 (Bar Chart)
- 각 항목이나 범주의 도수나 상대도수를 막대의 길이로 해당 값 표현
- 비교가 용이함
- x축은 범주
- y축은 빈도나 값
ex) 여러 제품의 판매량 비교, 여러 국가의 인구 수 비교
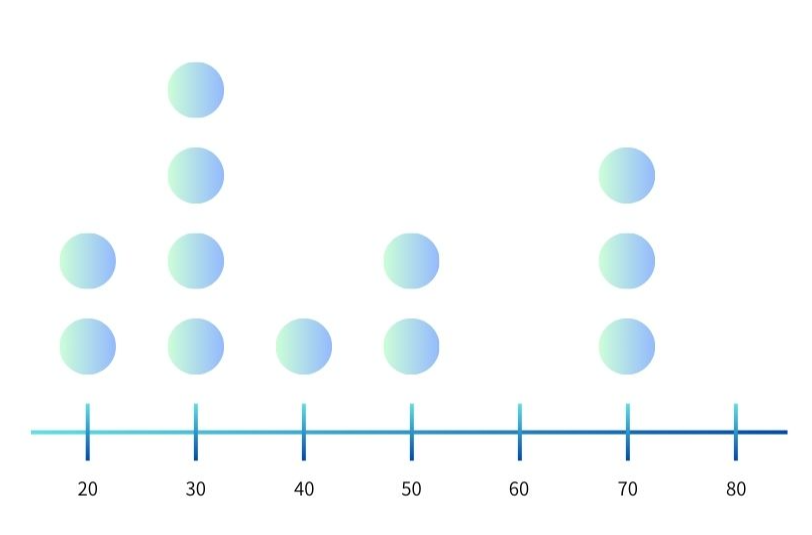
- 점도표 (Dot plot)
- 각 데이터를 점으로 표현하여 데이터 분포를 나타냄
- 각 관측값 위치에 점을 표시하고,
같은 관측값은 위로 누적
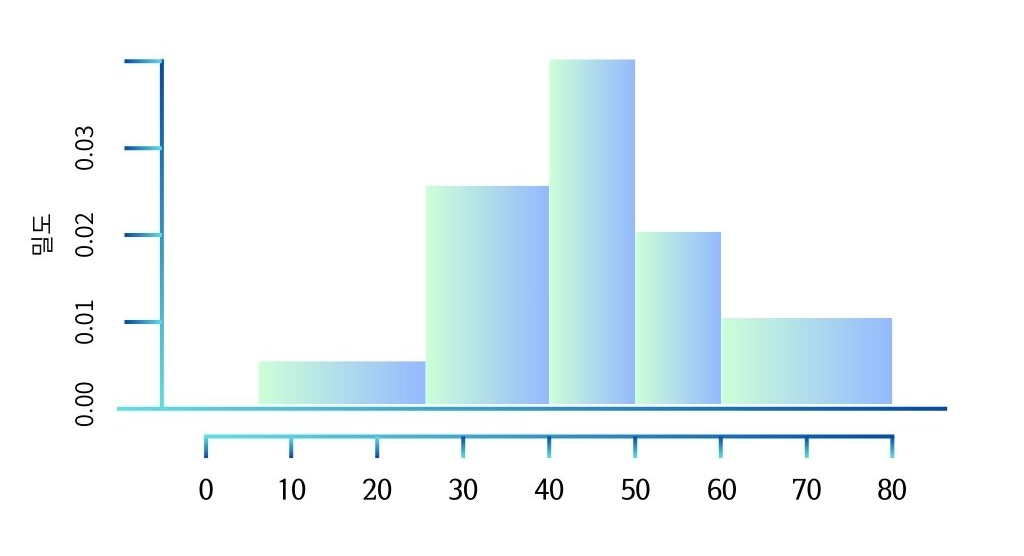
- 히스토그램 (Histogram)
- 연속형 데이터의 분포로 밀도추정을 시각화하는 그래프
- 데이터를 계급(Class)로 나누고,
각 계급에 속한 데이터의 빈도를 막대 높이로 나타냄
- 막대그래프와는 x축의 의미가 다르고, 막대의 순서는 임의적임
- 막대 사이에 간격이 없으며, 막대는 연속적 순서임
- 구간 설정에 따라 모양이 조금씩 달라짐
- x축 : 계급 (데이터범위) = 연속적인 값의 구간
- y축 : 빈도 (계급에 속한 데이터의 수)
- 줄기-잎 그림 (Stem-and-leaf plot)
- 각 데이터를 분해하여 숫자를 줄기와 잎으로 나타냄
- 줄기 (Stem) : 주로 10의 자리나 큰 자리 값
- 잎 (Leaf) : 주로 1의 자리나 작은 자리 값

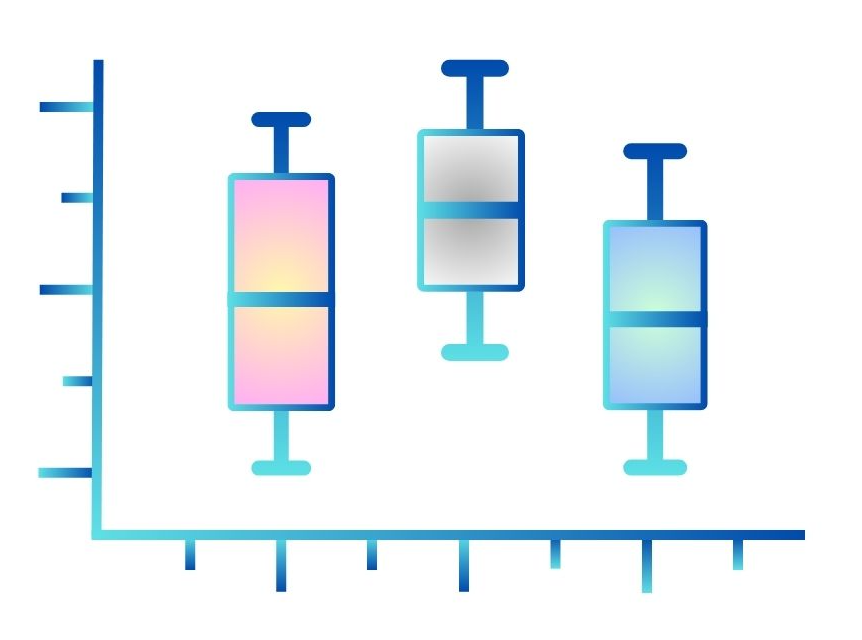
- 상자그림 (Box Plot)
- 중앙값, 사분위수, 최소값, 최대값을 한눈에 볼 수 있고,
이상치(Outlier)를 확인하는데 유용함
- 개별 값을 볼 수 없어서 전체 데이터를 확인할 때는 불편함
- 상자 : 데이터의 중간을 나타내는 사분위수 범위
- 중앙값 : 데이터의 중앙값은 상자 내부에서 수평선으로 표시
- 수염 (Whisker) : 데이터의 최소값과 최대값을 나타내며, 상자 외부로 뻗어있는 선
- 이상치 (Outlier) : 수염 외에 위치한 값
- 범주화
- 데이터를 특징에 따라 집단으로 나누는 것
- 계급(Class)의 수와 경계값(크기) 결정
- 복잡한 데이터를 간단하게 요약가능
- 서로 다른 항목을 비교하거나 분석이 쉬움
- 계급(Class) : 연속형 데이터를 일정구간으로 나눈 범주
- 경계값(Boundary) : 각 계급을 구분하는 값
- 계급의 수 결정
- 제곱근 방법
- 간단하고 빠르게 계급 수 결정 가능
- 공식 : k = √n ( k = 계급 수, n = 데이터 개수) - Sturges 공식
- n이 증가해도 계급 수가 급격히 늘어나지 않도록 설계
- 데이터가 정규분포를 따른다는 가정을 기반
- 공식 : k = 1 + 3.322 log10(n) - Rice 공식
- 데이터 개수가 많을수록 더 많은 계급 수 제안
- 데이터가 대규모일 때 적합
- 제곱근 방법
- 계급의 경계
- 간격(크기)와 시작점과 끝점 지정
- 기본은 동일 간격
- 자료의 구조와 설명을 고려해 선택
- 계급의 경계 설정법
- 최소값과 최대값
- 데이터의 최소값(min)과 최대값(Max) 구함
ex) 데이터 {12, 18, 24, 35}
→ 최소값 : 12
→ 최대값 : 35 - 계급 크기 결정
- 계급 크기 h = (최대값 - 최소값) / 계급 수 - 계급 경계값 설정
- 첫 계급의 하한은 최소값
- 이후 각 계급의 경계를 계급 크기만큼 증가시킴
- 최소값과 최대값
- 계급의 수 결정
반응형
'데이터 사이언스' 카테고리의 다른 글
| 기초통계학 4 | 분할표, 비교그림, 산점도, 공분산 & 상관계수 (0) | 2025.01.04 |
|---|---|
| 기초통계학 3 | 자료의 중심위치, 산포, 분포 형태 분석 (0) | 2025.01.04 |
| 기초통계학 1 | 모집단, 표본, 표본추출방법, 가중치 (3) | 2025.01.02 |
| 수리통계학 | 기초 용어 개념 정리 (2) | 2024.12.30 |
| 데이터 분석과 코딩 | 무료 플랫폼 (2) | 2024.12.28 |



